計算 (算数) はいわゆる「積み上げ学習」の教科で、たし算・ひき算・かけ算・わり算と、知識が関連して連続していきます。
それだけに、どこか一か所でつまづくと、以降の単元全部がわからなくなってしまう可能性がありますが、反面、きちんと理解できていれば学年に関係なくどんどん先に進んでいける教科でもあります。
「おさらい先生」の計算 (算数) は
ひき算ができないのはたし算の、わり算ができないのはかけ算の習熟不足、という考え方に基づき、各単元をマスターしないと先に進めない設計になっています。
学校の授業についていけず、短期間で学力を向上させたい生徒に向きますが、自習で進めるので、学年を追い越すこともできます。
- 「代数計算」に特化したカリキュラム
- 最短コースで学力を伸ばす、無学年ステップアップ構造の問題配列
- 多くの生徒がつまずく「分数」を徹底カバー
- できるようになるまで、徹底して反復させて実力が定着
端末の横向き・縦向き
どちらの表示にも対応 !
- 横向き
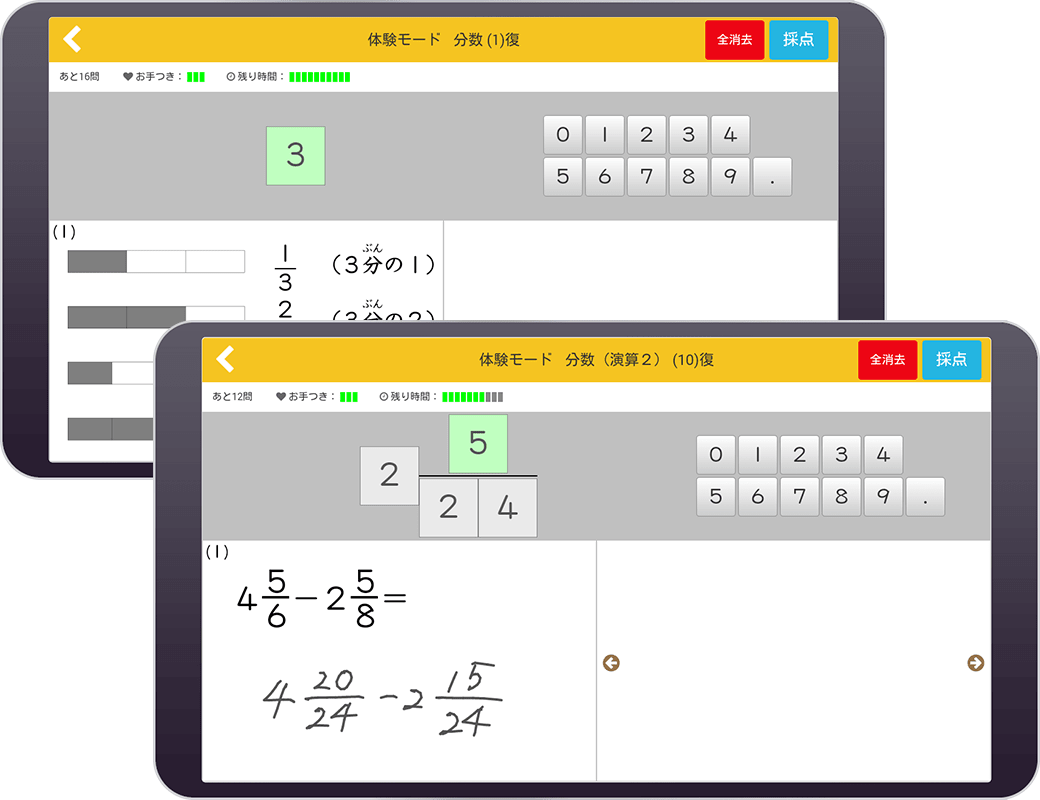
- 縦向き

計算 (算数) の教材構成
おさらい先生の計算 (算数) は、効率良く学習できるように無学年制で23のステップに分かれています。「診断モード」というテストにより生徒の実力を測り、23のステップの中から最適なスタート地点を見つけます。
- つぎのかず
(たす1~10まで 19+9=など) - 逆のかずかぞえ
(ひく1~10まで) - たしざん
(たして10~50) - ひきざん
(2ケタ-1~2ケタまで) - 足し算の筆算
(3ケタ+1~3ケタまで) - 引き算の筆算
(3ケタ-3ケタまで) - 掛け算 (九九)
(九九) - 掛け算 (筆算1)
(3ケタ×3ケタまで) - 掛け算 (筆算2)
(3ケタ×3ケタまで) - 割り算
(あまりある割り算まで) - 割り算 (筆算1)
(3~6ケタ÷3ケタまで) - 割り算 (筆算2)
- 割り算 (筆算3)
- 分数
(帯仮分数の変換) - 分数 (演算1)
- 分数 (演算2)
- 分数 (演算3)
(分数の割り算まで) - 小数1
- 小数2
(小数の割り算まで) - 四則混合1
(3コの分数の加減から四則混合算) - 四則混合2
- 四則混合3
- 四則混合4
- 正負の数1
(正負の数 加減) - 正負の数2
(正負の数 乗除) - 正負の数3
(式の値) - 正負の数4
(文字式 加法減法) - 方程式1
- 方程式2
(移項) - 連立方程式
- 文字式
(文字式 乗法除法) - 因数分解1
(式の展開) - 因数分解2
(式の展開の逆) - 因数分解3
- 平方根1
- 平方根2
(平方根の四則計算) - 二次方程式1
- 二次方程式2
(平方根 解の公式含む)
計算 (算数) の学習例
必要なところを必要なだけ反復
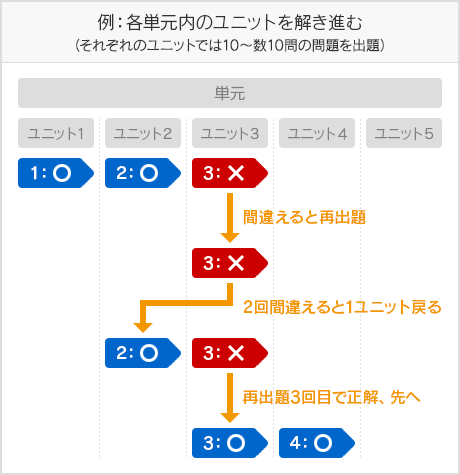
右下の図は、1、2(青色)のユニット(※)が順調に進んだ生徒が、ユニット3(赤色)でつまずいています。
ユニット3は計4回もチャレンジして突破、ユニット4へと進んでいます。
この生徒にとっては、ユニット3の「4回」という回数が習熟のための必要な反復回数だったと言えます。やり直すたびに正確性もスピードも向上し、習熟に近づきます。
※「おさらい先生」では、各単元内の問題集ひとつひとつを「ユニット」と呼びます。
生徒事例
学習実例を見てみましょう。中学1年生の生徒が、約9ヶ月でわり算から四則混合の計算までをリカバリーした例です。
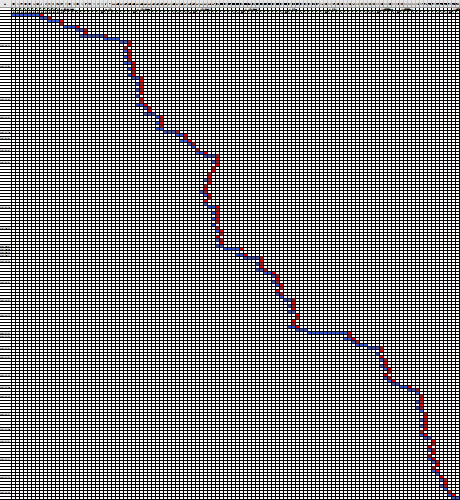
進度グラフは右下のようになりました。
進んでは(青)、繰り返したり戻ったり(赤)を繰り返しながら、根気強くおさらいしてきたことがわかります。
小学校分野の基礎計算を習熟しただけですが、中学での偏差値も大きく伸ばしました。
- 「おさらい先生」を体験したい
- 今すぐ「お試し版」で体験!




